Los algoritmos estudiados en este trabajo se pueden dividir en dos categorías:

• Exactos: Realizan una evaluación exacta de la medida requerida.
• Estimativos: Realizan una estimación de la medida en base a métodos de simulación.

Todos los algoritmos requieren de la evaluación de la función de estructura, que toma un red (o más bien un estado de la red en cierto instante determinado, definido por los componentes de la misma que en ese instante funcionan) y evalúa en 1 si la red se encuentra en estado operativo y 0 en caso contrario.
En nuestro caso particular, el estado de la red depende del estado de sus componentes (nodos y aristas que pueden estar o no en funcionamiento), y se considera un estado como operativo cuando se cumple la condición de conexidad (entre todo  par de nodos, entre s y t, o entre todo par de terminales del conjunto K, dependiendo de la medida de interés). Una red se considera también en estado no operativo cuando al menos un terminal no funciona (definición coherente, [6] y [2]). La verificación de la conexidad de la red se efectúa en base a una recorrida en profundidad. La descripción del algoritmo para la  evaluación de la función de estructura es la siguiente:

Este algoritmo realiza el cálculo exacto de la medida de confiabilidad generando todos los 2^|V|+|E| estados posibles del grafo y evaluando cuales son operativos. Para aquellos que lo son se acumula su probabilidad de ocurrencia (calculada como el producto de las probabilidades de los componentes que funcionan y los complementos de las probabilidades de los que no funcionan). En otras palabras, se acumulan las probabilidades de todos los estados que suman en la probabilidad del suceso "la red se encuentra en estado operativo". Para su implementación se utiliza la técnica de Backtracking.

La complejidad del algoritmo es O(2^|V|+|E|) ya que se deben generar todos los etados posibles del grafo.

Dado un grafo G, un estado o subgrafo G' de G en un instante particular queda definido por los componentes originales de G que en ese instante funcionan. La idea de este algoritmo se basa en obtener una estimación del valor de la confiabilidad R de la red mediante el sorteo de N estados G'_i del grafo original G. En definitiva, la confiabilidad de la red se calcula como la frecuencia de ocurrencia del suceso "todos los nodos terminales funcionan y están conectados entre sí".  La esperanza de este estimador es igual a R y la varianza es R(1-R)/N (esperanza de la suma de N variables de Bernoulli independientes e identicamente distribuídas), la cual se estima mediante la expresión R_est(1-R_est)/(N-1), donde R_est es la estimación obtenida y N es la cantidad de replicaciones.

El algoritmo implementado recibe el grafo, un identificador de semilla para el generador de números seudo-aleatorios y la cantidad de replicaciones N. Se utiliza para todas las replicaciones el mismo torrente de números seudo-aleatorios ya que el período del generador es lo suficientemente grande (se utiliza la biblioteca estándar drand48 incluída en el lenguaje C).

La complejidad del algoritmo es O(|V|+|E|). Se puede ver observando que se debe realizar un sorteo para cada nodo y arista más una recorrida en profundidad, la cual tiene una complejidad lineal en la cantidad de nodos del grafo.

El algoritmo Monte Carlo estándar produce resultados aceptables para redes de mediana confiabilidad, pero para redes altamente confiables se deben realizar muchas replicaciones para obtener estados no operativos (la cantidad de replicaciones necesarias para obtener un resultado para una precisión dada, es inversamente proporcional a la anti-confiabilidad de la red).

En [3] se propone este algoritmo, que reduce el problema original a un problema en una red más pequeña construida a partir de la original, condicionada a uno de sus cortes. El proceso es recursivo y se detiene cuando la red se encuentra siempre en estado operativo o no operativo, independientemente del estado de sus componentes. La construcción del método se realiza para obtener una estimación de la medida Q_k (anti-confiabilidad para un conjunto K de terminales), pero se puede generalizar para todas las restantes.

• Red K-conexa: una red G=(V,E) con un conjunto de terminales asociado KÍV es K-conexa cuando existe por lo menos un camino entre todo par de nodos del conjunto K (red en estado operativo).
• Q(G): anti-confiabilidad de G (probabilidad de que la red G no sea K-conexa).
• Un conjunto D Ì VÈE es un K-corte extendido de G si la subred G'=(V - D, E - D) no es K-conexa.
• Para una arista e Î E en G=(V, E) con terminales en K, G - e es la red cuyo conjunto de nodos es V y cuyo conjunto de aristas se obtiene a partir de E eliminando e. El conjunto de terminales de G - e es igual a K.
• Para un nodo v Î V en G=(V, E) con terminales en K, G - v es la red cuyo conjunto de nodos es V - {v} y cuyo conjunto de aristas se obtiene a partir de E eliminando todas las aristas incidentes a v. El conjunto de terminales de G - v es igual a K - {v}.
• Sea G=(V, E) con terminales en K y d un componente (nodo o arista) de la misma. Se denota G | d a la red derivada de G seteando la probabilidad de funcionamiento de d a 1 (d será un componente perfecto).
• Sea G=(V, E) con terminales en K y d un componente (nodo o arista) de la misma. Se denota G * d a la red derivada de G seteando la probabilidad de funcionamiento de d a 1. Si luego se halla una arista e=(v₁, v₂) (si d es una arista será e=d; si d es un nodo será v₁=d ó v₂=d) tal que r_e=r_v1=r_v2=1 se debe realizar la contracción de la misma, esto es, eliminando e, fundiendo sus extremidades v₁ y v₂ en un nuevo nodo w y seteando el nuevo conjunto de terminales a K - {v1, v2}È{w} si v₁ o v₂ pertenece a K, o simplemente K si ninguno es terminal.

Para una red G donde los terminales no fallan sean:

• D = {d₁, d₂, ..., d_|D|} un K-corte extendido en G
• A_D el evento "todos los componentes en D fallan"
• Q_D = probabilidad del evento A_D (producto de las probabilidades de falla de los componentes que lo forman)
• B_i el evento "todos los componentes en D_i = {d₁, d₂, ..., d_i-1} fallan y d_i funciona"
• G_i = (G - d₁ - ... - d_i-1) * d_i
• V variable aleatoria discreta independiente de las Y(G_i) con

Esta Propiedad muestra que la variable aleatoria Z tiene la misma esperanza, y menor varianza que la original Y. A grandes rasgos, la justificación de la igualdad (a)  se obtiene observando que el suceso A_D y los sucesos B_i constituyen una partición del suceso "la red se encuentra en estado no operativo" cuya probabilidad Q se desea calcular, y utilizando el teorema de probabilidades totales; la reducción de varianza se puede ver observando que en la estimación de la medida Q, siempre se tienen en cuenta estados de falla (suceso A_D). Una justificación detallada de estas demostraciones se puede ver en [8] para el caso particular de R_st).

En base a lo anterior, se construye en forma recursiva la siguiente variable aleatoria F:

y el siguiente algoritmo denominado RVR para obtener una muestra de F para una red G :

Algoritmo RVR

1 - Chequear fin de recursión:
        Si G es siempre K-conexo (|K|=1)    retornar 0
        Si G no es K-conexo (evaluando la función de estructura)    retornar 1

2 - Encontrar un K-corte extendido D de G: D = {d₁, d₂, ..., d_|D|}

3 - Calcular Q_D (probabilidad de que todos los componentes en D fallen)

4 - Sortear una muestra v de la variable aleatoria V

5 - Construir G_V =  (G - d₁ - ... - d_v-1) * d_v    (eliminaciones y contracción)

6 - Paso recursivo: retornar Q_D + (1 - Q_D)*RVR(G_V)
 
 

Ejemplo

El siguiente ejemplo muestra la ejecución del algoritmo RVR en una red con tres nodos (de los cuales dos son terminales) y dos aristas. La computación se muestra en forma de árbol, donde los hijos de un nodo interno son los posibles resultados del sorteo de la variable aleatoria V (los sucesos B_i). Las hojas del árbol corresponden a situaciones donde se cumple alguna condición de parada (red siempre K-conexa o no K-conexa). Una replicación del algoritmo solamente genera un camino desde la raíz hasta alguna hoja.

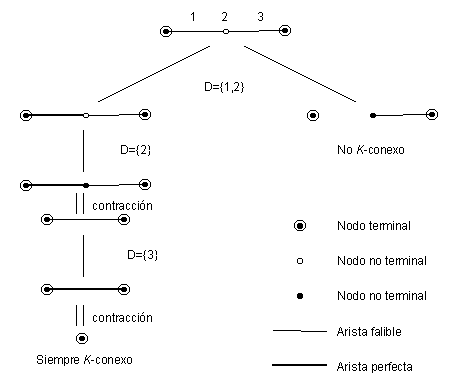
Se puede ver que en cada paso recursivo, el problema original se reduce a uno (y solo uno) más pequeño, ya que en el paso 5 del algoritmo se reduce la cantidad de componentes de la red original (mediante eliminaciones y contracciones). Así, la cantidad de invocaciones recursivas se puede acotar por |V|+|E| y observando que la operación más costosa en cada paso es la evaluación de la función de estructura fi (de orden O(|V|)), el orden del algoritmo RVR tendrá orden de complejidad O(|V| * (|V|+|E|)).

Para realizar varias replicaciones de la simulación, el algoritmo anterior es invocado varias veces mediante una iteración. La esperanza de F(G) se estima mediante el cociente de la suma de los resultados de todas las replicaciones sobre la cantidad de las mismas:

que por comodidad para su cálculo se puede llevar a

El algoritmo implementado para el cálculo de la confiabilidad utilizando RVR recibe el grafo, un identificador de semilla para el generador de números seudo-aleatorios (se utiliza de la misma forma que en MCC) y una cantidad N de replicaciones.