Pruebas de eficiencia
El objetivo de estas pruebas es comparar
la performance del algoritmo RVR frente a otros conocidos (básicamente
MCC). También interesa estudiar para que casos particulares (de
topologías, confiabilidades elementales, probabilidades de cortes)
el algoritmo tiene comportamientos diferentes en términos de error
relativo y tiempos de ejecución. Se utilizaron topologías
particulares y valores particulares para las confiabilidades de los componentes.
Las topologías seleccionadas
son las siguientes:
-
ARPANET
-
Grafo bipartito completo
con fuente y terminal
-
Red telefónica
de fibra óptica de Montevideo
-
Dodecaedro
-
Malla dispersa
-
Malla densa
A continuación se describen brevemente
cada una de las topologías, las pruebas realizadas y los resultados
obtenidos. Estos se presentan en tablas conteniendo valores de confiabilidad,
varianza, tiempos de ejecución y eficiencia relativa (producto de
los cocientes de varianzas y tiempos: W = Var * T). Esta última
medida se utiliza para comparar la performance general entre algoritmos.
Para todos los casos de prueba, los
algoritmos se corrieron en una estación de trabajo Sun sparc Enterprise
250 con 256 Mb de memoria RAM y procesador de 250 Mhz, bajo el sistema
operativo SunOS 5.7, con relativamente baja carga de trabajos. Los fuentes
fueron compilados utilizando el compilador C++ de GNU (gcc versión
2.95) con la opción de optimización de código de 64
bits. Los casos de prueba se generaron de la misma forma que para las pruebas
de validación. Los algoritmos estimativos se corrieron con 104
replicaciones (salvo indicación). Los resultados de tiempos de ejecución
se muestran en segundos. Al final de esta página se muestran las
conclusiones
generales de todas las pruebas de eficiencia.
Caso 1: ARPANET
Topología de la red de computadoras
que dio origen a la actual Internet. El objetivo principal de este caso
de prueba es comparar la evolución de los tiempos de ejecución
de cada algoritmo en relación al tamaño de la red así
como determinar el tamaño aproximado de una red para la cual es
factible utilizar el algoritmo GCE. Las topologías fueron tomadas
de [12] y [2]
y constituyen la evolución de la red desde su surgimiento en 1969
hasta 1979. Se realizaron pruebas con valores 0,9 para las probabilidades
de funcionamiento de nodos y aristas. La medida de interés en este
caso es RV. Las características de cada topología
(cantidad de nodos y aristas) se muestran en la siguiente tabla.
|
Topología
|
|V|
|
|E|
|
|
Dic. 69
|
4
|
4
|
|
Jul. 70
|
8
|
10
|
|
Mar. 71
|
15
|
19
|
|
Abr. 72
|
23
|
26
|
|
Set. 72
|
34
|
38
|
|
Año 79
|
58
|
69
|
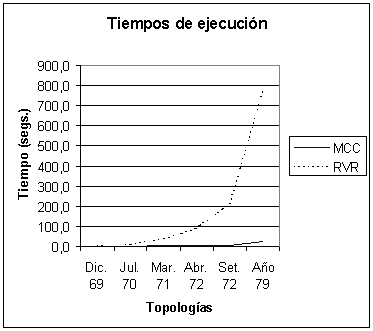
Conclusiones
-
Claramente los tiempos de ejecución
crecen (en función del tamaño de la red) en forma más
acentuada para el algoritmo RVR.
-
La conclusión más importante
extraída de las pruebas con este caso es que el algoritmo GCE resulta
impracticable para una red con 15 nodos y 19 aristas (y por lo tanto, también
para redes de mayor tamaño).
Caso 2: Grafo bipartito
completo con fuente y terminal
Se considera un tipo particular de
grafo de conectividad relativamente alta, donde interesa la medida
Rst.
La topología consiste en un grafo bipartito completo más
dos terminales, cada uno de los cuales es adyacente a todos los nodos de
una partición. Los objetivos de este caso de prueba son los mismos
que para el caso anterior. También interesa estudiar la evolución
de la confiabilidad con el aumento de las cardinalidades de las clases
V1 y V2 de la bipartición.
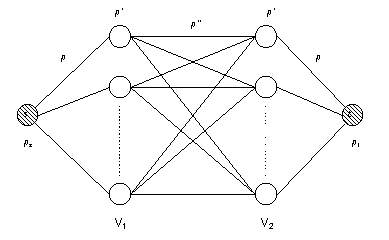
Los resultados y conclusiones son
similares a los del caso anterior.
Caso 3: Red telefónica
de fibra óptica de Montevideo (1992)
Esta topología es una versión
parcial de la red telefónica de fibra óptica de Montevideo
(año 1992). Los datos son tomados de [10],
donde se cuenta con resultados numéricos. Está formada por
14 nodos y 21 aristas. La medida de interés en este caso es RV.
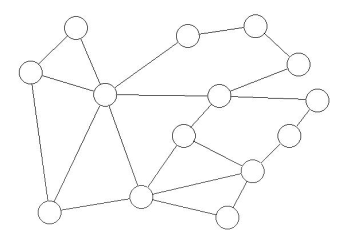
El principal objetivo de este caso
de prueba es realizar comparaciones con resultados obtenidos en trabajos
anteriores. Se realizaron en total 36 pruebas variando las probabilidades
de funcionamiento de nodos y aristas sobre el conjunto de valores {0,9-0,95-0,98-0,99-0,999-1,0}.
Conclusiones
-
Un resultado interesante para esta prueba
tiene que ver con la estimación de la confiabilidad de la red con
valores de confiabilidad 1 en nodos y 0,999 en aristas. Para esta prueba,
el algoritmo MCC obtuvo una media de 1 con varianza 0 en una red que no
es perfecta, mientras que RVR obtuvo un valor muy cercano a 1 con una pequeña
varianza.
También se realizaron comparaciones
con resultados obtenidos en trabajos anteriores, en particular para los
algoritmos de Ahmad (algoritmo exacto, [20])
y Antitético Generalizado [10]
donde se realizaron pruebas con nodos perfectos y confiabilidades en aristas
para los valores 0,9-0,99-0,999 con 105, 106, 107
replicaciones respectivamente. Los resultados obtenidos son coherentes
con los existentes, y en la siguiente tabla se muestra una comparación
de los errores relativos para estas tres pruebas.
|
Antitético
|
RVR
|
|
6,9E-03
|
7,3E-03
|
|
2,9E-02
|
2,4E-02
|
|
9,5E-02
|
7,6E-02
|
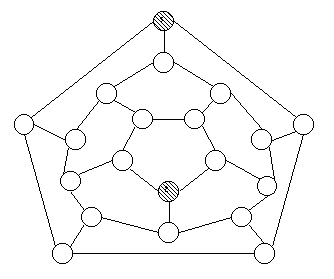
Caso 4: Dodecaedro
Topología de red encontrada
en varios trabajos anteriores como caso de prueba (20 nodos y 25 aristas).
En [10] se cuenta con resultados numéricos
para la medida RV y en [8]
para Rst. El objetivo de este caso es realizar cálculos
para las dos medidas de interés, comparar con resultados de trabajos
anteriores y comparar errores relativos y eficiencias relativas para MCC
y RVR. Se realizaron 36 pruebas con el mismo esquema del caso anterior.
Los resultados más interesantes
de las pruebas con esta topología tienen que ver con la comparación
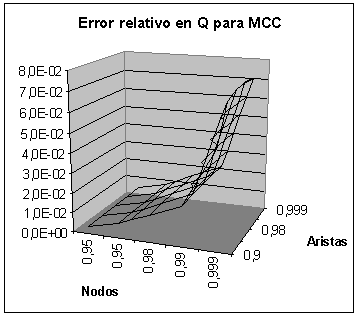
de los errores relativos para MCC y RVR en el cálculo de QV
y Qst.
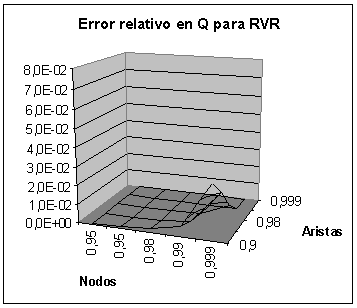
Resultados para QV
Conclusiones
-
Se puede observar que para RVR existen
menos zonas donde los errores son altos. En particular estos se dan para
confiabilidades medio-bajas para aristas y medio-altas para nodos, mientras
que para MCC se dan para confiabilidades altas en nodos y cualquier confiabilidad
en aristas.
-
También se puede ver que los
errores para RVR (máximo igual a 3,0E-02) son menores que para MCC
(máximo igual a 7,0E-02).
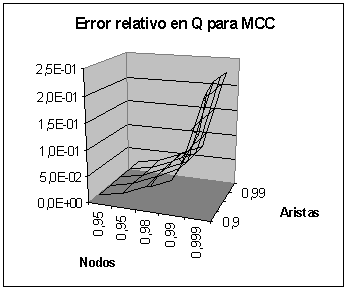
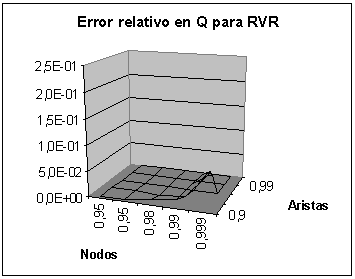
Resultados para Qst
Conclusiones
-
En general se observan las mismas zonas
de precisión para el cálculo de Qst
que para Qv en ambos algoritmos.
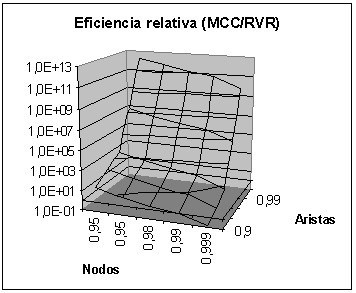
Eficiencias relativas (Qv
y Qst)
Conclusiones
-
Para Qv, se puede
observar que para confiabilidades bajas en nodos y altas en aristas el
trabajo de MCC es mayor, mientras que para confiabilidades altas en nodos
y bajas en aristas el trabajo es mayor en RVR y en general para redes muy
confiables es mayor el trabajo para MCC.
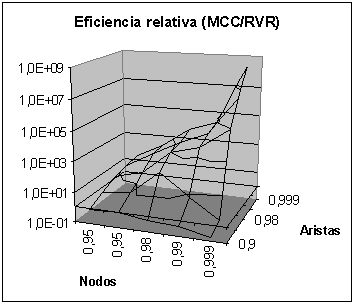
-
Para Qst, se puede
observar que la zona donde el trabajo es mayor para RVR es la misma que
para Qv (nodos muy confiables y aristas poco confiables)
mientras que cambian las zonas de mayor esfuerzo para MCC (observar que
el pico corresponde a redes muy confiables lo que confirma la conveniencia
de RVR para redes de este tipo).
Caso 5: Malla dispersa
Se considera una topología de red con forma de malla (10x10 nodos
más 5 terminales y 127 aristas), tomado de [11]
donde se cuenta con resultados numéricos. La medida de interés
en este caso es Rk. Los dos objetivos principales de
este caso son realizar pruebas con topologías con confiabilidades
dispares en sus componentes (se distinguen entre aristas horizontales,
verticales y terminales), y comparar con los resultados obtenidos en el
trabajo original.
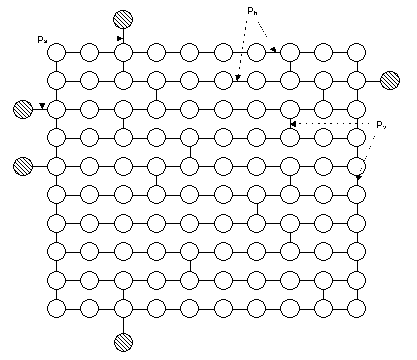
Para este caso se realizaron pruebas
con valores particulares (tomados del trabajo original) para las confiabilidades
de las aristas. Se extrajeron las siguientes conclusiones:
-
El algoritmo MCC da prácticamente
los mismos valores para cambios sensibles en las confiabilidades de las
componentes de la red (no es el caso de RVR).
-
Las eficiencias relativas muestran en
todos los casos mayor trabajo para RVR. Esto se debe al tamaño relativamente
grande de la red que hace que los tiempos de ejecución sean tan
altos que no compensen la reducción de la varianza.
En la comparación con los resultados
originales se encontraron ciertas discrepancias con los obtenidos en nuestro
trabajo (ver informe).
Caso 6: Malla densa
Topología similar a la anterior,
pero con 90 aristas verticales (10x10 nodos más 5 terminales y 180
aristas). La medida de interés también es Rk
(siendo K el mismo conjunto de terminales que para el caso anterior).
El objetivo de este caso de prueba es observar el aumento de la confiabilidad
de la red al aumentar la cantidad de aristas y también el aumento
de los tiempos de ejecución.
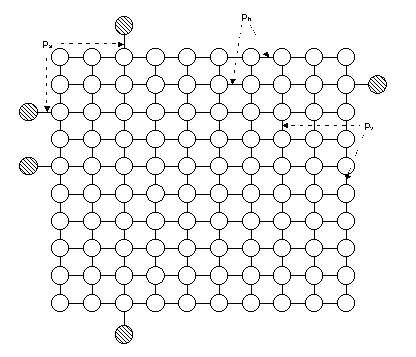
Se realizaron pruebas con el mismo
conjunto de valores para las confiabilidades elementales que para el caso
anterior. Las principales conclusiones extraídas son las siguientes:
-
En general los tiempos de ejecución
no aumentaron demasiado (insignificante para MCC y del orden del 2% para
RVR).
-
Las confiabilidades aumentaron en algunos
casos y en otros disminuyeron, pero se debe tener en cuenta también
las varianzas y no solos las medias. En particular se puede observar que
los valores de las medias siempre aumentan al aumentar las confiabilidades
de los componentes, pero no al aumentar la densidad de la red (si bien
teóricamente el valor exacto de la confiabilidad de la red debería
aumentar). Esto se puede justificar en los casos de Rk
y en particular Rst, donde la inserción de una
nueva arista entre un par de vértices no adyacentes no siempre contribuye
en formar caminos alternativos a los ya existentes entre terminales.
Conclusiones generales
Las principales conclusiones generales
extraídas de todas las pruebas realizadas son las siguientes:
-
El algoritmo GCE se hace impracticable
para redes de tamaño aproximado a 15 nodos y 19 aristas.
-
Las varianzas de RVR son siempre menores
que las de MCC y esta diferencia se acentúa al aumentar la confiabilidad
de la red.
-
Los tiempos de ejecución de RVR
son siempre mayores que los de MCC y la diferencia aumenta al aumentar
el tamaño de la red.
-
Los resultados de confiabilidad en MCC
son menos sensibles a los cambios en las confiabilidades de los componentes,
que en RVR. Esto se puede justificar observando que al cambiar sensiblemente
la confiabilidad de un componente, los sorteos que determinan el funcionamiento
o no de un componente en MCC pueden dar el mismo resultado (que siempre
será 0 o 1); este no es el caso de RVR, donde se tienen en cuenta
más valores exactos (probabilidad de falla del corte elegido) en
la estimación de la medida.
-
Los errores relativos para ambos algoritmos,
en una determinada topología, son mayores para ciertos valores de
confiabilidades de nodos y aristas (ver caso de prueba 4 -Dodecaedro-).
Las zonas de errores relativos son distintas para distintas medidas (Qv
y Qst en el mismo ejemplo).
-
En algunos casos se presentaron errores
de precisión numérica, en particular en el cálculo
de varianzas en RVR para redes muy confiables.
-
En general los resultados obtenidos
son coherentes con los obtenidos en trabajos anteriores, salvo para el
caso 5 (malla dispersa) donde se observaron diferencias importantes.
-
Los resultados obtenidos para las confiabilidades
del caso 6 (malla densa) muestran (en relación a los obtenidos para
el caso 5 -malla dispersa-) que no siempre un aumento en la cantidad de
componentes de la red (aristas en este caso) se ve reflejado en un aumento
en las medias de confiabilidad obtenidas con los algoritmos estimativos.
En estos casos se debe prestar especial atención a las varianzas
y construir los intervalos de confianza.