Experimentos con aritmética de precisión finita
La computadora sólo puede almacenar de forma exacta una cantidad finita de números. Si queremos almacenar un número que no es representable de forma exacta, lo que hace la computadora es almacenarlo en el número representable más cercano (mediante aproximación por redondeo).
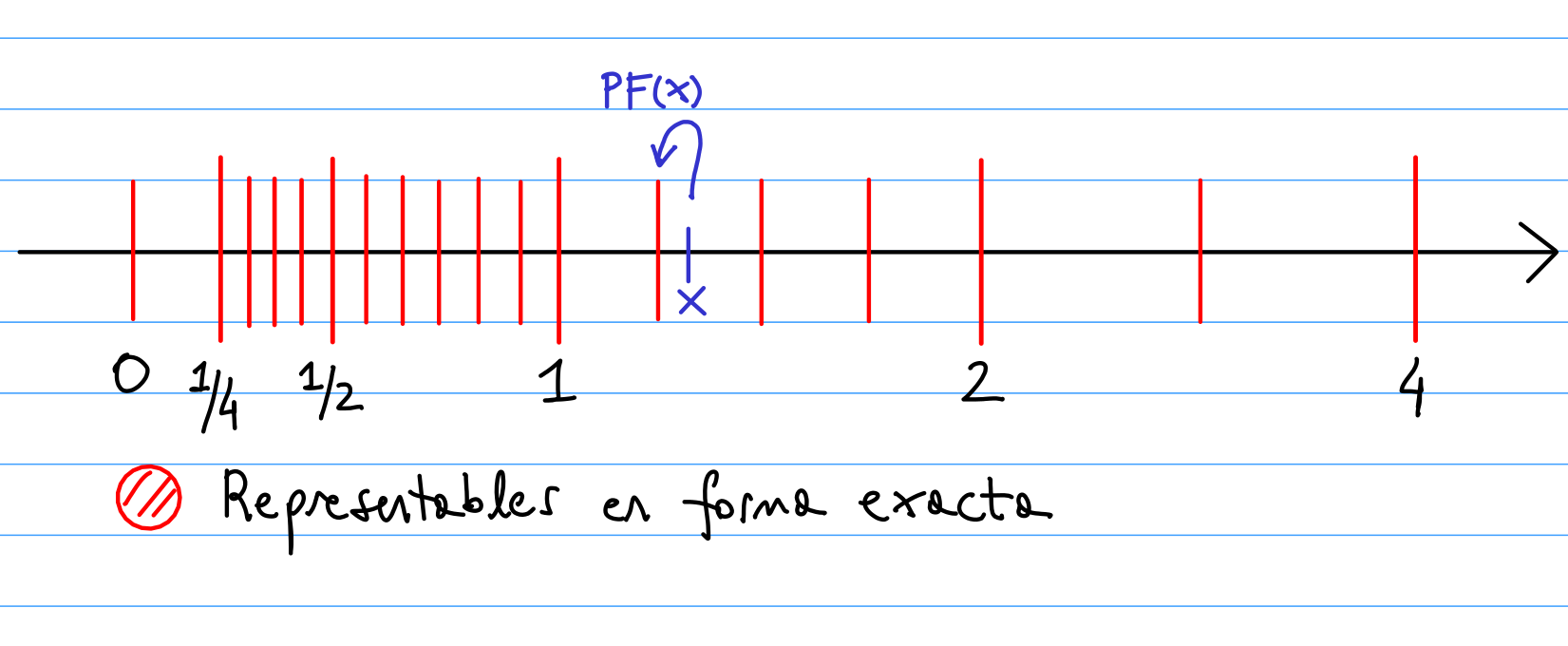
Esta aproximación se traduce en errores al realizar operaciones, que en algunos casos pueden ser considerables.
Asociativa no funciona
Consideremos la función identidad $ f(x)=x $. En aritmética exacta, esta se puede escribir en forma equivalente como: $$ g(x) = ( 1 + x ) - 1 .$$ Sin embargo, en aritmética de precisión finita, estas expresiones no son equivalentes. El siguiente gráfico muestra la diferencia entre ambas expresiones, en una parte de su dominio.
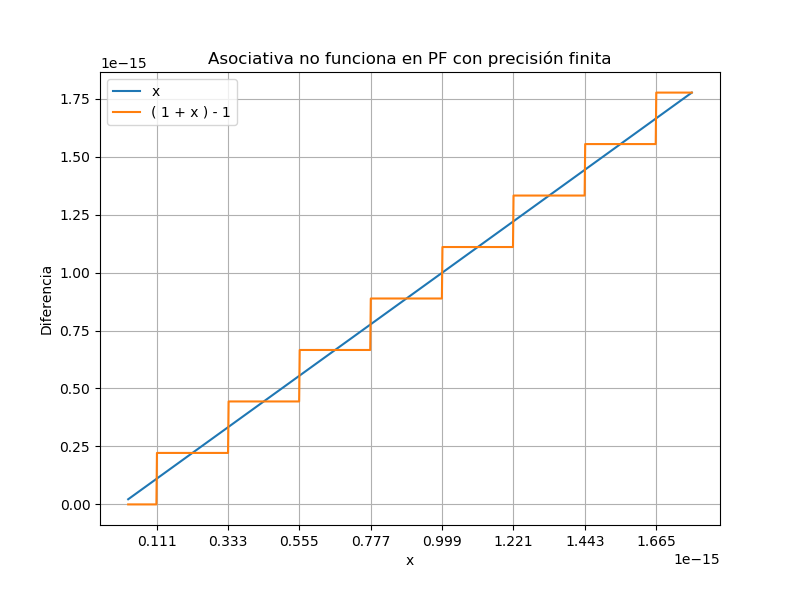
El comportamiento anterior se explica por los “huecos” entre los números representables de forma exacta. La distancia entre números representables (el ancho de los huecos), es siempre un múltiplo de una constante, denominada “épsilon de máquina”. Esta constante se puede definir como la distancia entre el número 1 y el siguiente número representable, a la derecha del 1. Usando punto flotante con precisión doble, esta constante es: $$ \epsilon_m = 1 \times 2^{-52} \simeq 2.2204 \times 10^{-16} .$$
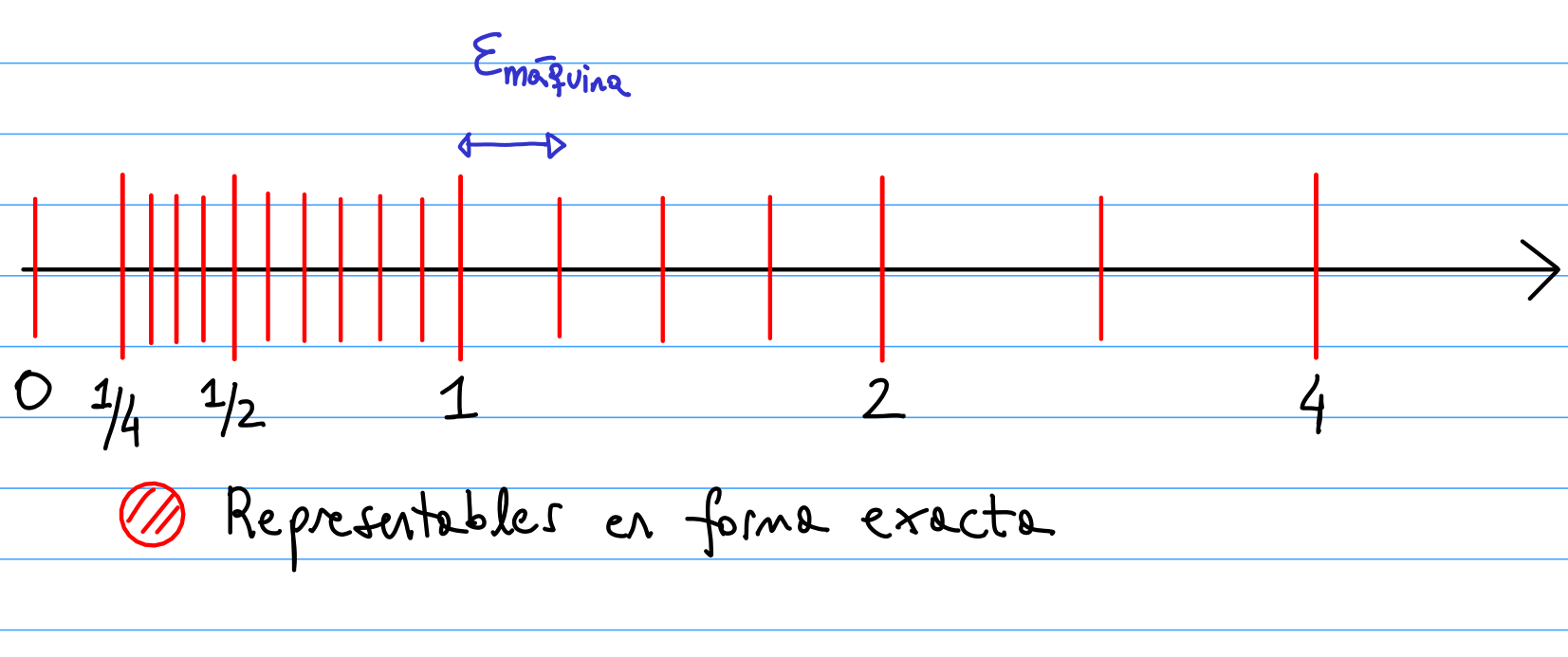
Teniendo en cuenta esto, y denotando mediante $PF(z)$ al número representable en el cual se almacena $z \in \mathbb{R}$, se puede ver que se cumple: $$ PF(1+x) = 1, \quad \forall \quad 0 \leq x < \epsilon_m / 2 .$$ Esto explica que el gráfico de la función $g(x) = ( 1 + x ) - 1$ sea nulo en todo el intervalo $[0, \epsilon_m / 2]$. El cambio en el valor de $PF(1+x)$ se da recién para $x > \epsilon_m / 2$, cuando pasa a valer: $1+\epsilon_m$. A partir de ahí la función $g$ se mantiene constante nuevamente. El siguiente salto se da en el punto medio entre $1+\epsilon_m$ y el siguiente numero representable a su derecha, y así sucesivamente.
Cancelación catastrófica
Consideremos la función $ f(x) = \sqrt{x+1} - \sqrt{x} $. Para valores de $x$ “grandes”, los sumandos de esta expresión se parecen cada vez más. Debido a esto, es posible que la computadora los almacene con el mismo valor de punto flotante. Esto haría que los términos se cancelen (en punto flotante), y la función tome el valor nulo; aunque en aritmética exacta la función es siempre positiva.
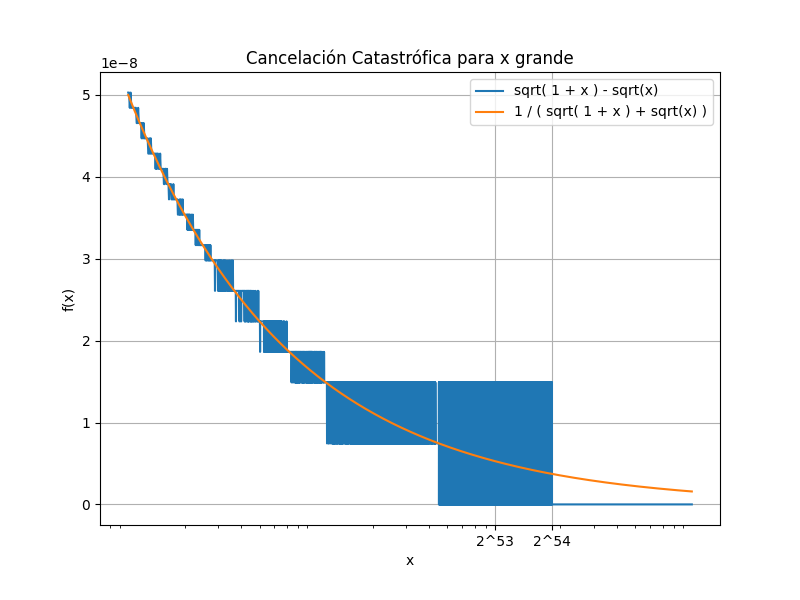
Una forma de evitar este fenómeno, conocido como “cancelación catastrófica”, es utilizar una expresión alternativa para la función. Por ejemplo, multiplicando y dividiendo la expresión original de $f$ por $\sqrt{x+1} + \sqrt{x}$, se obtiene: $$ g(x) = \left( \sqrt{x+1} - \sqrt{x} \right) \frac{ \sqrt{x+1} + \sqrt{x} }{ \sqrt{x+1} + \sqrt{x} } = \frac{ 1 }{ \sqrt{x+1} + \sqrt{x} } .$$ En aritmética exacta, ambas expresiones son equivalentes: $f=g$. Sin embargo, $g$ tiene la ventaja de que no involucra una resta de términos de valores cercanos, que se podrían confundir al usar precisión finita.
El siguiente gráfico muestra la diferencia entre ambas expresiones, para valores “grandes” de $x$. Es claro que la expresión $g$ (naranja) tiene un mejor comportamiento con respecto a $f$ (azul). En particular, el gráfico de $g$ tiende a cero, aunque no se anula nunca. En este sentido presenta el mismo comportamiento que en aritmética exacta.
Distancias entre representables
En Python, el comando $spacing(x)$, del paquete numpy, nos dice cuál es la distancia entre $x$ y el siguiente número representable a su derecha. Así, por ejemplo: $spacing(1)=\epsilon_m \simeq 2.2204 \times 10^{-16}$. La siguiente imagen corresponde al gráfico de esta función, para $x$ variando en el intervalo $[1/2,10]$.
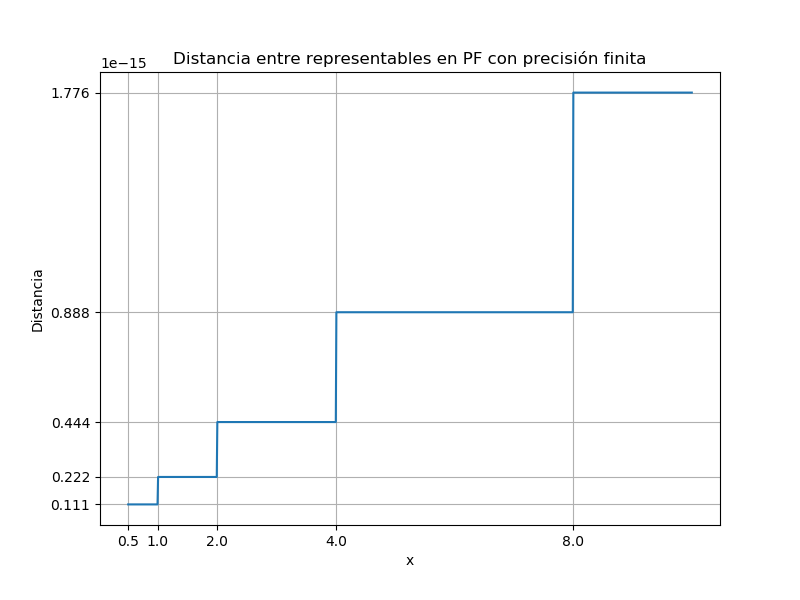
Como se puede ver, la distancia es constante entre potencias de $2$. En particular: en el intervalo $[1,2]$, la distancia entre los números representables es siempre igual al épsilon de máquina $\epsilon_m$. En el intervalo $[2,4]$, la distancia entre representables es igual a $2 \epsilon_m$; en el intervalo $[4,8]$, la distancia es igual a $4 \epsilon_m$, etc. En general, se puede probar que:
En el intervalo $[2^i,2^{i+1}]$, la distancia entre representables es constante, y es igual a $2^i \epsilon_m$.
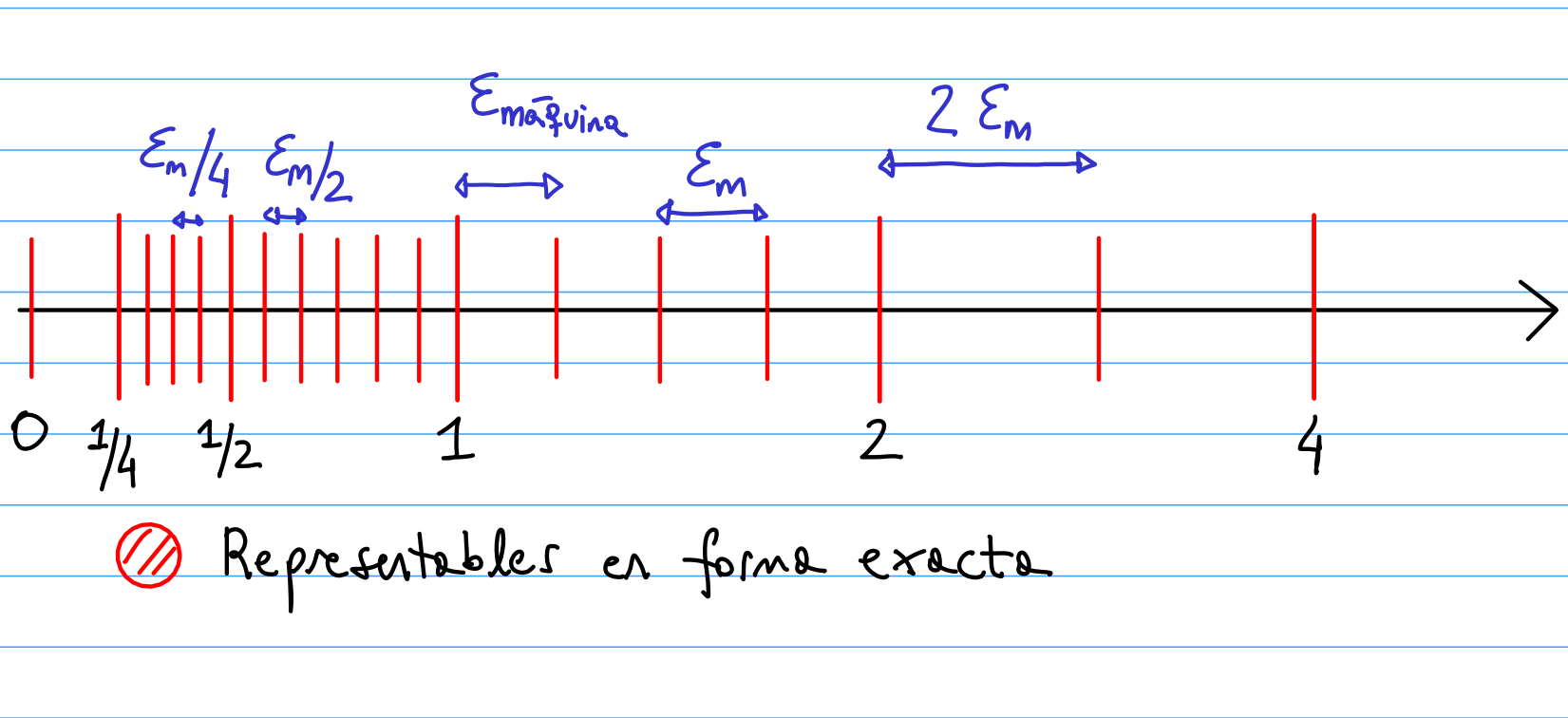
Esto se puede explicar teniendo en cuenta la forma en que se representan los números en el sistema de punto flotante de base 2 (binario), con precisión finita. Esta forma es: $$ PF(x) = (-1)^s \times 1.a_1 a_2 \ldots a_{p-1} a_p \times 2^e, \quad a_i \in \left\lbrace 0 , 1 \right\rbrace .$$
Para pasar de un número representable al siguiente, hay que sumar 1 al bit menos significativo (el bit más a la derecha de la coma). Si se tienen $p$ dígitos, el peso de este bit es: $2^{-p} \times 2^e = \epsilon_m \times 2^{e}$. Por otro lado, el exponente $e$ es constante en cada intervalo de potencias de 2 consecutivas $[2^i,2^{i+1}]$, y vale $i$.